An evidential classifier based on Dempster-Shafer theory and deep learning

An evidential classifier based on Dempster-Shafer theory and deep learning
Abstract
提出了一种基于Dempster-Shafer (DS)理论和卷积神经网络(CNN)结构的集值分类器。在这个证据深度学习分类器中,卷积层和池化层首先从输入数据中提取高维特征。然后将特征转换为质量函数,并在DS层中采用Dempster规则进行聚合,最后,期望效用层基于质量函数进行集值分类。
1.Introduction
在机器学习中,分类是指基于标记实例的训练集预测新样本类别的任务。最常见的分类问题是精确分类,在这种分类中,一个样本被分为且仅属于一个可能的类。不幸的是,在高度不确定性的情况下,这种困难的分配往往会导致错误的分类。
在本研究中,我们基于Dempster-Shafer (DS)理论和深度卷积神经网络(CNN)提出了一种新的集值分类器,称为证据深度学习分类器。在该分类器中,使用深度CNN从原始数据中提取高阶特征。然后,将特征导入到基于距离的DS层中构造质量函数。最后,利用质量函数计算分配给一组类的行为的效用,以进行集值分类。整个网络使用端到端学习过程进行训练。个网络使用端到端学习过程进行训练。此外,我们提供了一个策略,只考虑30个类中的一些子集,而不是考虑所有的类。使用三种类型的数据集(图像、信号和语义关系)演示和讨论了分类器的有效性及其决策策略。本研究的主要贡献是证明了由于增加了额外的DS层,cnn可以增强集值分类和新颖性检测能力,同时在35个精确分类任务中保持良好的性能.
Related work
在过去的二十年里,DS理论被越来越多地应用于模式识别和监督分类,主要有三个方向。第一种是分类器融合,将多个分类器的输出转换为信念函数,并通过合适的组合规则进行聚合。另一个方向是证据校准:分类器的决策被转换为具有某种频率校准特性的质量函数。最后一种方法是设计证据分类器,它将输入特征的证据分解为基本质量函数,并通过Dempster规则将它们组合起来。证据分类器的输出可用于决策。在实践中,证据分类器的性能主要取决于两个方面:训练数据集和对象表示的可靠性。
Yuan等人提出了一种使用DS理论来衡量决策过程中深度神经网络输出的不确定性的方法,但在使用来自深度学习模型的特征作为证据分类器的输入,为决策生成信息质量函数输出以允许集值分类方面,似乎仍然做得很少。
2. Background
2.1. Dempster-Shafer theory
DS 证据理论(Dempster-Shafer envidence theory)也称为DS理论。是一种处理不确定性问题的完整理论。D-S算法就是对不确定信息处理的一个理论工具,是用于对不确实信息做智能处理和数据融合典型方法。
通俗理解
有一个村庄失窃了,抓到了两个嫌疑人A和B,那么一共有四种情况:A和B都没有偷窃,A是小偷,B是小偷,A和B合伙作案。现在有三个证人村民,他们只是看到了整个案件的部分过程,并没有全部的目击真个现场,所以对究竟是哪一个情况,有不同的判断,判断结果用概率表示(概率越大那么表示该情况发生的概率越大):
结果 | 村民1 | 村民2 | 村民3 |
null | 0 | 0 | 0 |
A | 0.96 | 0.02 | 0.04 |
B | 0.03 | 0.97 | 0.02 |
A or B | 0.01 | 0.01 | 0.94 |
而DS理论要解决的问题就是,如何综合这三个村民提供的证据来判断到底属于哪一种情况。
理论中的基本概念
1、识别框架(或称为假设空间):一个非空集合,包含两两互斥事件。就是我们要判断事件发生情况的范围,上面那个例子中,识别空间就是:A和B都没有偷窃,A是小偷,B是小偷,A和B合伙作案这四种情况;
2、基本概率分配(Basic Probability Assignment,BPA):确定每一个村民对这个四种情况分别对应的概率判断为多少。也就是确定每一个证人对每一种情况的基本概率为多少。可以看出:同一个证人(村民)对不同情况的概率判断之和应该为1;对于null(就是都不是)的判断都为0。而这个分配概率称之为mass函数,(把几个证人(这里指的是村民)的概率判断进行组合,称之为组合mass,)。
3、信度函数(belief function):某个事件的信度函数指的是该事情所有的子集概率之和。
4、似然函数(plausibility fuction):某事件的似然函数指的是与该事件交集不为空的概率之和。
2.2. Evidential neural network
在 ENN 分类器中,输入向量与原型的接近程度被认为是其所属类别的证据。这些证据被转换成 mass 函数,并使用 Dempster 规则进行组合。
我们考虑一个训练集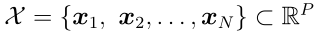 (N个用P维特征向量表示的例子)和一个由N个原型
(N个用P维特征向量表示的例子)和一个由N个原型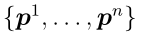
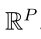 组成的ENN分类器。对于一个测试样本x, ENN分类器构造质量函数来量化关于它的类的不确定性
组成的ENN分类器。对于一个测试样本x, ENN分类器构造质量函数来量化关于它的类的不确定性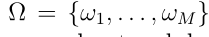 ,使用三步过程。这个过程可以在神经网络层中实现,这个三步过程定义如下。
,使用三步过程。这个过程可以在神经网络层中实现,这个三步过程定义如下。
Step 1: 计算x和每个参考模式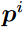 之间基于距离的支持为:
之间基于距离的支持为:
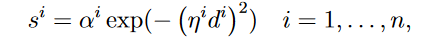
其中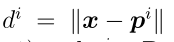 是x和原型
是x和原型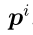 之间的欧氏距离,
之间的欧氏距离,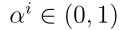 和
和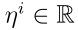 是与原型
是与原型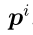 相关的参数。原型向量
相关的参数。原型向量 可认为是输入层与包含n个径向基函数(RBF)单位隐层之间的连接权向量。
可认为是输入层与包含n个径向基函数(RBF)单位隐层之间的连接权向量。
Step 2: 与参考模式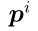 相关的质量函数
相关的质量函数![]() 计算为:
计算为:
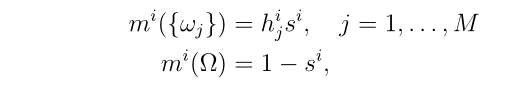
上式可视为计算ENN分类器第二隐层中单元的激活,该隐层由n个模块组成,每个模块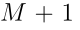 个单元。模块i的结果对应于
个单元。模块i的结果对应于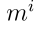 分配的信念质量。
分配的信念质量。
其中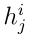 为原型
为原型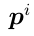 与类
与类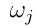 的隶属度,且
的隶属度,且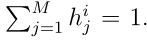
我们将由原型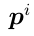 引起的质量向量表示为
引起的质量向量表示为
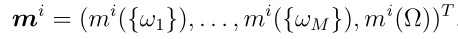
Step 3:n个质量函数![]() ,i = 1,…, n,根据Dempster规则进行聚合。组合质量函数迭代计算为
,i = 1,…, n,根据Dempster规则进行聚合。组合质量函数迭代计算为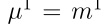 ,
,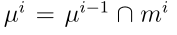 ,对于
,对于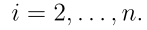 有:
有:
 对于
对于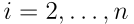 和
和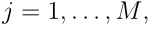
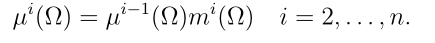
ENN分类器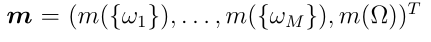 的输出最终为:
的输出最终为:
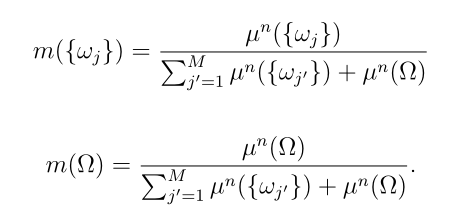
2.3. Feature representation via deep CNN
在实践中,ENN分类器的有效性在很大程度上取决于其输入特征中所包含的信息。特征表示是机器学习工作流程的一个重要部分,包括从原始数据中发现分类所需的预测器。
深度cnn是一种特殊的多层神经网络,是应用最广泛的深度学习体系结构之一。最常见的cnn由卷积层、池化层和完全连接层组成。卷积层和池化层被定义为阶段。阶段将其输入数据转换为中间表示,作为特征提取器工作。一般来说,深度CNN由几个堆叠的阶段组成,这些阶段处理原始数据并重复地将它们转换为更高级别的特征映射。然后,完全连接的层作为决策者,根据特征映射将输入分配给其中一个类。因此,深层CNN中堆叠阶段的最终输出可以看作是输入数据的特征表示。在研究中,这些高级特征被用作DS层的输入,能够集值分类。
为了理解深度cnn的特征表示,我们简要回顾了卷积层和池化层的过程。考虑一个输入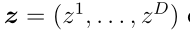 由D输入映射或输入通道
由D输入映射或输入通道 大小H × W。卷积层由几个从z中提取特征映射的卷积核组成。卷积核是一个小矩阵,用于对每个输入映射应用卷积操作,通过在映射上滑动,对输入映射中内核当前所在的部分执行element-wise乘法,将相乘的结果相加为单个值,然后将核的偏置与求和值相加。因此,由e个大小为a × b的卷积核组成的卷积层中的过程表示为:
大小H × W。卷积层由几个从z中提取特征映射的卷积核组成。卷积核是一个小矩阵,用于对每个输入映射应用卷积操作,通过在映射上滑动,对输入映射中内核当前所在的部分执行element-wise乘法,将相乘的结果相加为单个值,然后将核的偏置与求和值相加。因此,由e个大小为a × b的卷积核组成的卷积层中的过程表示为:
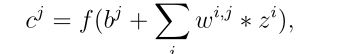
其中![]() 是第i个输入映射和第j个输出映射之间的卷积核;
是第i个输入映射和第j个输出映射之间的卷积核;![]() 为核
为核![]() 的偏置;*表示卷积操作;
的偏置;*表示卷积操作;![]() 是第i个输入映射,大小为H × W, i = 1,…D;
是第i个输入映射,大小为H × W, i = 1,…D;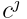 为第j个输出特征图,大小为
为第j个输出特征图,大小为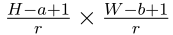
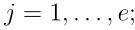 r是内核在输入映射
r是内核在输入映射![]() 上滑动的步幅;f为激活函数,具 有s × s非重叠局部区域的池化操作表示为
上滑动的步幅;f为激活函数,具 有s × s非重叠局部区域的池化操作表示为
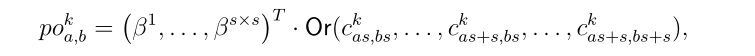
其中![]() 是第k个输出映射中的元素(a, b),位于第a行第b列;或者是一个从最大值到最小值的排序函数;表示点积(β1,…, βs×s)是池权向量,如最大池(β1, β2,…, βs×s) =200(1,0,…, 0)和均值池
是第k个输出映射中的元素(a, b),位于第a行第b列;或者是一个从最大值到最小值的排序函数;表示点积(β1,…, βs×s)是池权向量,如最大池(β1, β2,…, βs×s) =200(1,0,…, 0)和均值池

3. Proposed classifier
3.1节介绍了总体架构,包括几个阶段:用于特征表示的深度CNN、构造大量函数的DS层和用于决策的预期效用层。预期效用层的细节在第3.2节中描述,建议分类器的学习策略在第3.3节中公开。最后,3.4节介绍了选择部分多类行为的方法。
3.1. Network architecture
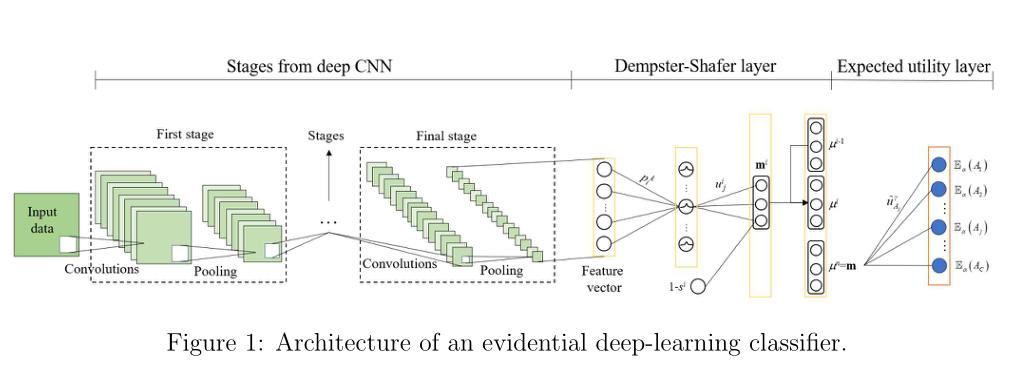
这项工作的主要思想是将2.2节中介绍的ENN分类器和2.3节中提到的CNN体系结构进行杂交,方法是在CNN的输出端“插入”一个DS层,后面跟着一个实用层。所提方法的体系结构称为证据深度学习分类器,如图1所示。证据深度学习分类器能够在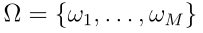 上执行集值分类并量化关于样本类别的不确定性,通过一个信念函数。信息在这个网络中的传播可以用以下三步程序来描述:
上执行集值分类并量化关于样本类别的不确定性,通过一个信念函数。信息在这个网络中的传播可以用以下三步程序来描述:
Step 1:输入样本被发送到CNN体系结构的几个阶段,以提取与分类相关的潜在特征,就像在概率CNN中所做的那样。在最后阶段,P维输出向量是样本的特征表示,准备作为输入发送到DS层。该体系结构提供了输入示例的健壮可靠的表示。由于这种表示,证据深度学习分类器在精确分类方面的性能与具有相同阶段的概率分类器相似,甚至更好。在精确分类任务中,证据深度学习分类器和概率深度学习分类器的性能比较将证明这种优势(Section 4)。
Step 2: 第1步计算的特征向量被输入到DS层,在DS层中被转换为通过Dempster规则聚合的质量函数,如2.2节所述。DS层的输出是一个(M + 1)质量向量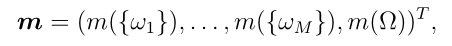 ,它表征了分类器对样本类概率的信念,量化了对象表示中的不确定性。质量
,它表征了分类器对样本类概率的信念,量化了对象表示中的不确定性。质量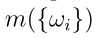 是样品属于ωi类的一个相信度。当特征表示包含混乱和冲突的信息时,DS层倾向于跨类均匀分配质量。额外的自由度
是样品属于ωi类的一个相信度。当特征表示包含混乱和冲突的信息时,DS层倾向于跨类均匀分配质量。额外的自由度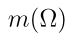 使得量化证据的缺乏和验证模型是否受过良好训练成为可能。DS层的优势将在Section 4中使用证据深度学习分类器进行集值分类的性能评估中得到验证。
使得量化证据的缺乏和验证模型是否受过良好训练成为可能。DS层的优势将在Section 4中使用证据深度学习分类器进行集值分类的性能评估中得到验证。
Step 3: 输出质量向量m被输入到用于决策的期望效用层,在那里它被用来计算行为的期望效用。每个行为被定义为将样本赋值给Ω的一个非空子集a。因此,如果考虑到所有可能的行为,预期效用层的输出是一个大小最多等于2M−1的预期效用向量。预期的实用层允许建议的分类器执行集值分类。这种能力将通过证据和概率深度学习分类器在集合值分类和新颖性检测任务中的性能比较来证明。
3.2. Expected utility layer
设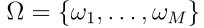 是类的集合。对于只有精确预测的分类问题,行为被定义为将一个例子分配给M类中的一个且仅一个类。行为的集合是
是类的集合。对于只有精确预测的分类问题,行为被定义为将一个例子分配给M类中的一个且仅一个类。行为的集合是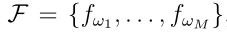 ,其中
,其中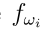 表示赋值给类
表示赋值给类![]() 为了进行决策,我们定义效用矩阵
为了进行决策,我们定义效用矩阵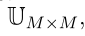 ,其通称
,其通称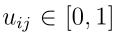 是当真正的类为
是当真正的类为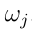 时,将一个例子赋给类
时,将一个例子赋给类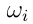 的效用。这里,
的效用。这里,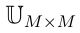 被称为原始效用矩阵。对于具有信念函数的决策,每个行为
被称为原始效用矩阵。对于具有信念函数的决策,每个行为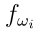 都能归纳出期望效用。
都能归纳出期望效用。
对于预测不精确的分类问题,Ma和denaunux提出了一种在不确定条件下进行集值分类的方法,方法是将行为集泛化为将样本部分分配给Ω的非空子集a。于是,行为集变成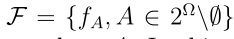 ,其中
,其中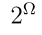 是Ω的幂集,
是Ω的幂集,![]() 表示对子集A的赋值。在本研究中,如果|A|≥2,则定义子集A为多类集。对于F的决策,将原始效用矩阵
表示对子集A的赋值。在本研究中,如果|A|≥2,则定义子集A为多类集。对于F的决策,将原始效用矩阵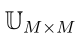 扩展到
扩展到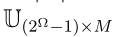 ,其中每个元素
,其中每个元素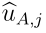 表示当真标签为
表示当真标签为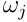 时,将样本分配给集合a的效用。
时,将样本分配给集合a的效用。
当真类为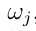 时,将样本分配给集合a的效用定义为a中每次精确分配效用的有序加权平均(OWA)聚合
时,将样本分配给集合a的效用定义为a中每次精确分配效用的有序加权平均(OWA)聚合
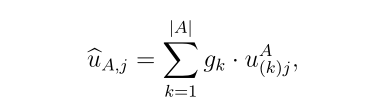
其中![]() 是由原始效用矩阵
是由原始效用矩阵 中的元素组成的集合
中的元素组成的集合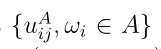 中的第k个元素,权值
中的第k个元素,权值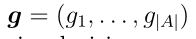 表示当分类器必须在一组可能的选择中做出精确决策时,选择
表示当分类器必须在一组可能的选择中做出精确决策时,选择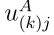 的偏好。权重向量g中的元素表示DM对不精度的容忍度。例如,当分配行为
的偏好。权重向量g中的元素表示DM对不精度的容忍度。例如,当分配行为 具有效用1,一旦设置A包含真标签,则对不精确的完全容忍就实现了,无论A有多不精确。在这种情况下,只考虑集合
具有效用1,一旦设置A包含真标签,则对不精确的完全容忍就实现了,无论A有多不精确。在这种情况下,只考虑集合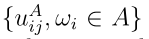 中元素的最大效用:
中元素的最大效用: 。在另一个极端,不给不精度赋值的DM会认为行为
。在另一个极端,不给不精度赋值的DM会认为行为 ;相当于从A中均匀随机选择一个类:
;相当于从A中均匀随机选择一个类:
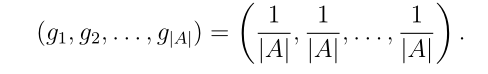
在本研究中,采用O 'Hagan的方法确定了OW A算子的权向量g。我们将不精密公差度定义为
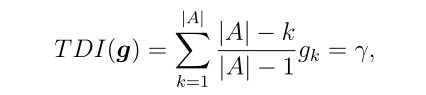
最大值等于1,最小值等于0,平均值等于0.5。在实践中,我们只需要考虑γ在0.5和1之间的值,因为当γ<0.5[38]时,精确分配比不精确分配更可取。给定一个γ值,我们可以通过最大化熵来计算OWA算子的权值
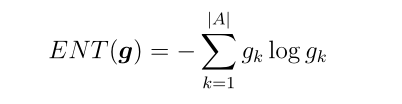
受限于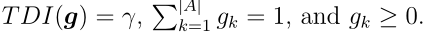
基于扩展效用矩阵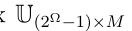 和DS层m的输出,我们可以用广义Hurwicz 准则计算一个行为的期望效用
和DS层m的输出,我们可以用广义Hurwicz 准则计算一个行为的期望效用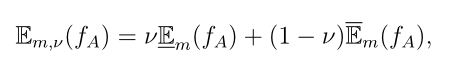
其中Em(fA)和Em(fA)分别是下期望值效用和上期望值效用:
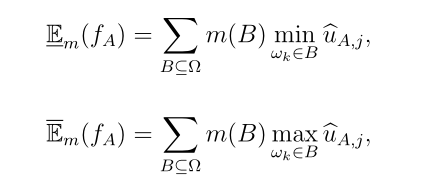
ν为悲观指数,被认为是该分类器的超参数。样本最终被分配到集合A使
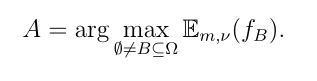
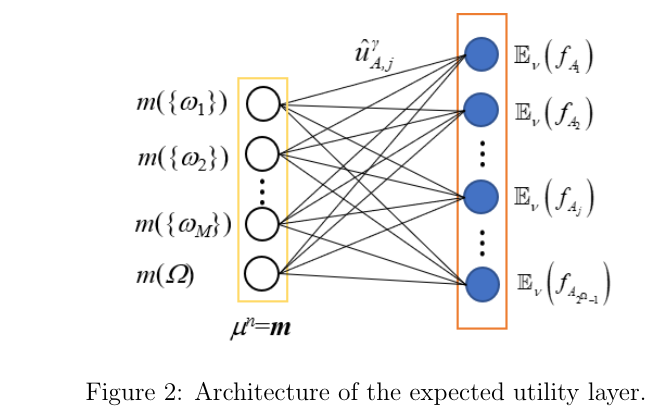
与DS层类似,使用utility理论将样本分配给F中的集合的过程可以概括为神经网络的一层,称为期望效用层,如图2所示。在这一层中,输入和输出分别是来自前面DS层的质量向量m和f中所有行为的预期效用。DS层的单元j与分配给集合A的输出单元 之间的连接权重为效用值
之间的连接权重为效用值 。由于描述不精度公差度的系数γ是固定的,因此在训练过程中不需要更新期望效用层的连接权值。
。由于描述不精度公差度的系数γ是固定的,因此在训练过程中不需要更新期望效用层的连接权值。
3.3. Learning
证据深度学习分类器可以通过随机梯度下降算法进行训练。给定一个带有类标签ω *的样本x,我们将预测损耗定义为
对于 ,当
,当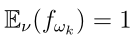 或者对于
或者对于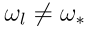 ,
, 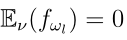 时,损失最小。
时,损失最小。
期望效用层误差 m的
m的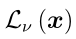 的导数为
的导数为
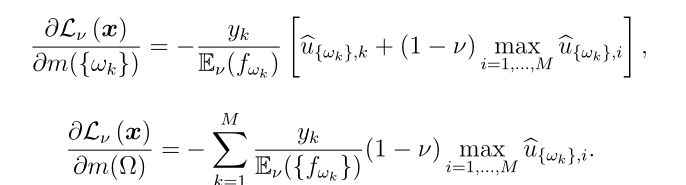
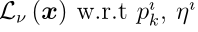 和
和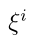 在DS层中的导数与Denœux的原始结果相同
在DS层中的导数与Denœux的原始结果相同
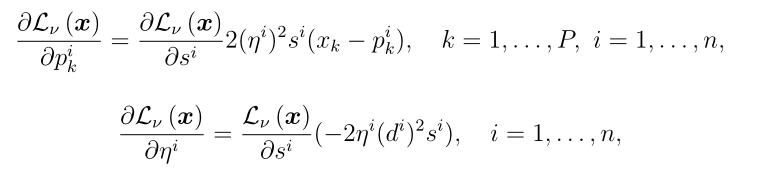
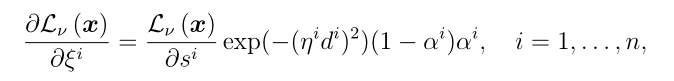
其中P为参考模式和输入特征向量的维度,n为原型的数量。
在所提出的分类器中,DS层连接到最后卷积阶段的池化层。因此,我们可以计算误差 和
和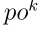 的导数为
的导数为
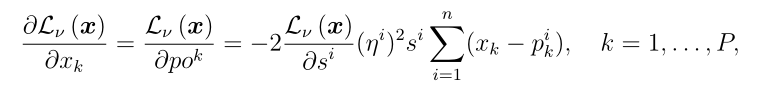
其中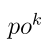 是最终池化层的第k个输出映射,是一个1 × 1张量。其余阶段中的错误传播在概率CNN中执行。
是最终池化层的第k个输出映射,是一个1 × 1张量。其余阶段中的错误传播在概率CNN中执行。
3.4. Act selection
如3.2所述,考虑多类赋值时的行为集为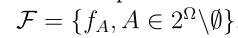 ,因为实例可以赋给Ω的任意非空子集A。然而,F的基数随着类的数量呈指数增长,当类的数量M较大时,可能会排除该方法的应用。
,因为实例可以赋给Ω的任意非空子集A。然而,F的基数随着类的数量呈指数增长,当类的数量M较大时,可能会排除该方法的应用。
在[62]中,证明了具有卷积层和DS层的神经网络在候选类相似(例如“猫”和“狗”或“马”和“鹿”)时倾向于将样本分配给多类集。因此,只考虑部分多类行为将样本分配给包含两个或两个以上相似类的子集可能是有利的。
在本研究中,我们提出了一种在识别框架下确定相似类的策略,并基于类相似度从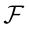 中选择部分多类行为。使用选择的部分多类行为,而不是
中选择部分多类行为。使用选择的部分多类行为,而不是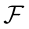 中的所有行为,我们可以减少集值赋值的计算成本。这种策略可以描述如下。
中的所有行为,我们可以减少集值赋值的计算成本。这种策略可以描述如下。
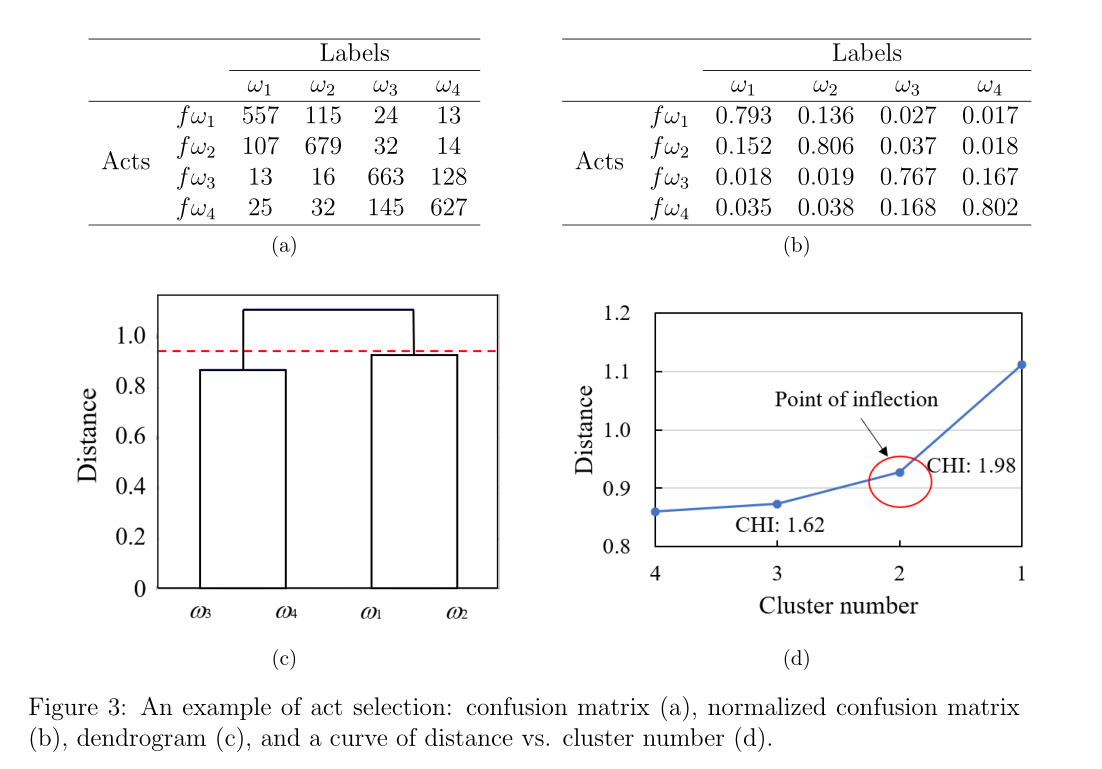
Step 1: 使用训练集,由经过训练的证据深度学习分类器生成一个只有精确分配的混淆矩阵。在混淆矩阵中,每一列代表一个类别中预测的样本分布。
Step 2: 使用混淆矩阵中的每一列的总数进行归一化。每一个归一化列都被视为对应类的特征。
Step 3: 计算每两个特征之间的欧氏距离,通过层次凝聚聚类(HAC)算法[6,56]生成树状图。每两个特征之间的距离表示两个类的相似度。如果两个类相似,则距离接近于0。
Step 4: 根据树状图绘制距离与集群数量的关系,如图3d所示。然后可以使用曲线中的拐点来确定切割树状图的阈值。在本研究中,我们使用Calinski-Harabasz指数(CHI)来确定这一点。拐点是曲线中CHI最大的拐点,右边的点有少量高度相似的类。这可以用HAC算法的性质来解释。非常相似的类在算法进行时首先进行合并。在HAC运行的最后,我们到达一个阶段,不同的类被留下来合并,但它们之间的距离很大;这些类并不相似,不需要在行为选择策略中进行集群。
Step 5: 以拐点对应的距离为阈值,切割树状图。类似的模式是距离小于阈值的集群组中的类。最后,选择与相似类对应的多类行为。
图3显示了一个行为选择示例,其中使用带有Ward链接的HAC算法生成树状图。图3d显示了一个拐点,其CHI为1.91,对应的距离为0.927。用该距离作为欧氏距离的阈值来切割树状图。有两对相似的模式:{ω1, ω2}和{ω3, ω4}。因此,所选的部分多类行为为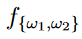 和
和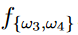 。
。
4. Experiments
4.1. Evaluation of set-valued classification
在证据深度学习分类器的应用中,我们使用扩展效用矩阵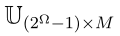 进行性能评价。对于数据集T,分类性能由平均效用评估为
进行性能评价。对于数据集T,分类性能由平均效用评估为
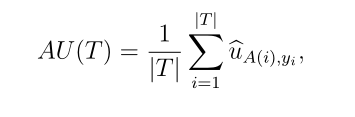
其中yi是学习示例i的真类,A(i)是使用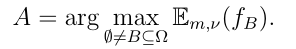 选择的子集,使用第3.2节介绍的表示法buA,yi是将样本i分配给子集A⊆Ω的效用,当其真类为yi时。仅考虑精确行为时,(21)定义的AU标准归结为分类精度。平均基数也计算为
选择的子集,使用第3.2节介绍的表示法buA,yi是将样本i分配给子集A⊆Ω的效用,当其真类为yi时。仅考虑精确行为时,(21)定义的AU标准归结为分类精度。平均基数也计算为
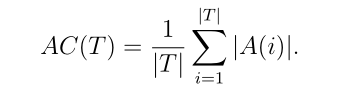
此外,我们还考虑数据集T0={T0O,T0I}由离群值子集T0O组成的情况,离群值的类别不属于识别框架Ω, 以及类所属的内层的子集T0IΩ. 我们比较f的速率Ω 在T0I和T0O中评估分类器拒绝异常值和模糊样本的能力。这种能力在[9]中被称为新颖性检测。通常,一个训练有素的分类器应该有很低的f值Ω 在T0I,但在T0O有很高的比率
在本研究中,我们将所提出的分类器与概率CNN进行了比较。为了确保公平的比较,我们在CNN中采用以下基于概率的集值分类策略:fA?∗ fA0当且仅当E(fA)≤ E(fA0),其中E(fA)=Pωk∈A p(ωk)·buA,k
